こんにちは.株式会社Ridge-iでインターンを務めていますmitsuhiko-nozawaです.本記事では,Gradient Compressionと呼ばれる,分散学習環境下で勾配の通信量を削減する手法について紹介します. なお本記事は@machinery81と@zawatsky_rによってレビューされています.
TL;DR
- Gradient Compressionについて簡単に紹介
- Gradient Compressionの派生手法を紹介
- Gradient Compressionの派生手法について,論文サマリを作成
Gradient Compressionとは
機械学習モデルの学習にかかる時間を短縮するための方法として,複数のノードを持つクラスタを用意し,各ノードにデータを分散させて並列で学習する分散学習が行われています.その際,各ノードで別々にモデルのパラメータを学習させると,ノードごとに異なるパラメータを持つモデルができてしまいます.そのため,各ノードで学習時に発生する勾配を蓄積し,同期の際に全ノードの持つ勾配の集約計算と再分配を行い,ノード毎に共通の勾配を持たせて学習することで,全ノードに同じパラメータを持たせるという方法がとられます.
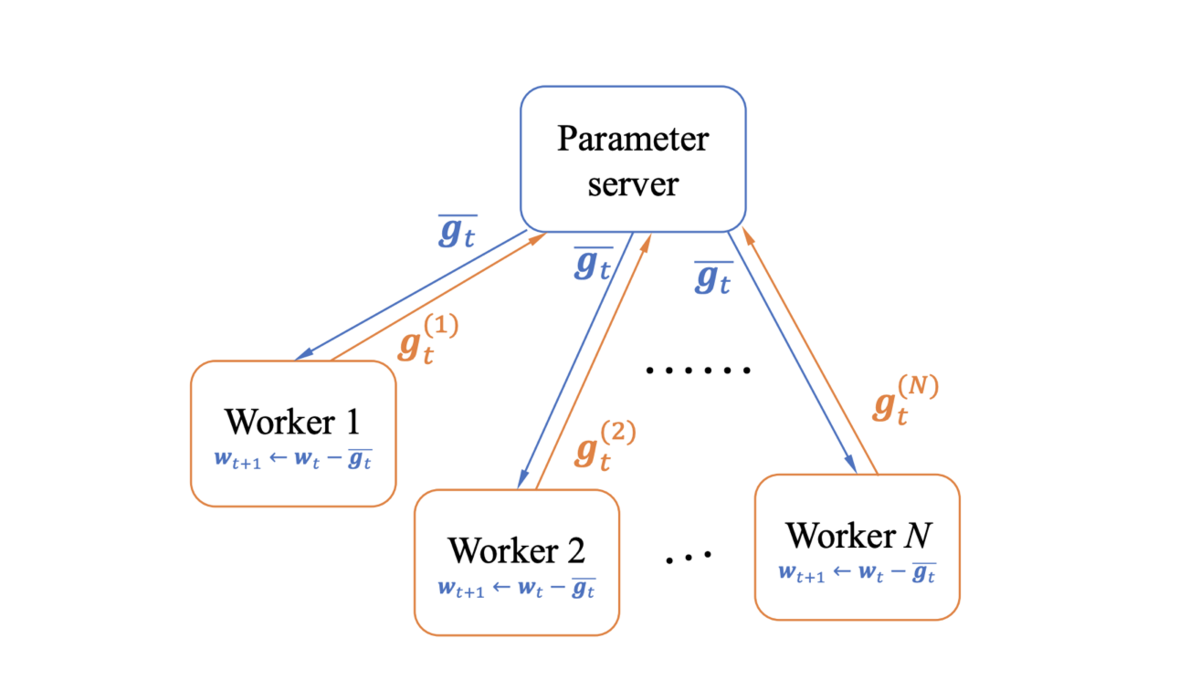
しかし,深層学習のようなパラメータ数が多いモデルでは,並列化するノード数が増えるほど,パラメータを同期(各ノードに勾配を集約・再分配)するための通信時間が,学習にかかる総時間に対して支配的となり,並列数に対して学習時間の短縮率がスケールしなくなるという問題があります.加えて,通信に必要な回線は帯域幅が大きくなるほど高価なものになります.そのため,パラメータの同期時間を短縮するための方法が盛んに研究されています.その中でもGradient Compressionは,通信する勾配の量を何らかの形で減らすことを目的とした手法になっています.
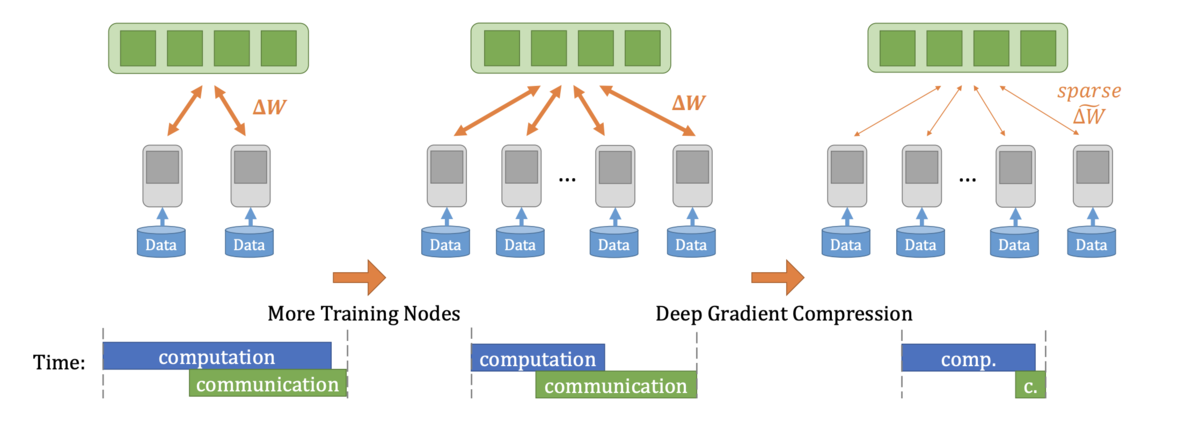
Gradient Compressionの概要
Gradient Compressionは,同期ステップでのノード間の勾配の通信量を何らかの形で削減する手法です.主な手法として,通信する勾配を閾値によって制限するGradient Sparsificationと,勾配そのものの精度を制限するGradient Quantizationの二つがあります. これらの手法では一般的に非可逆的な圧縮が行われるため,圧縮を行わない時のモデルの学習と同等の収束性を保障しないという問題があります.そのため,モデルの収束性と勾配の圧縮率のトレードオフを扱う必要があります. それぞれの手法について,詳しく説明していきます.
Gradient Compressionの分類
Gradient Sparcification
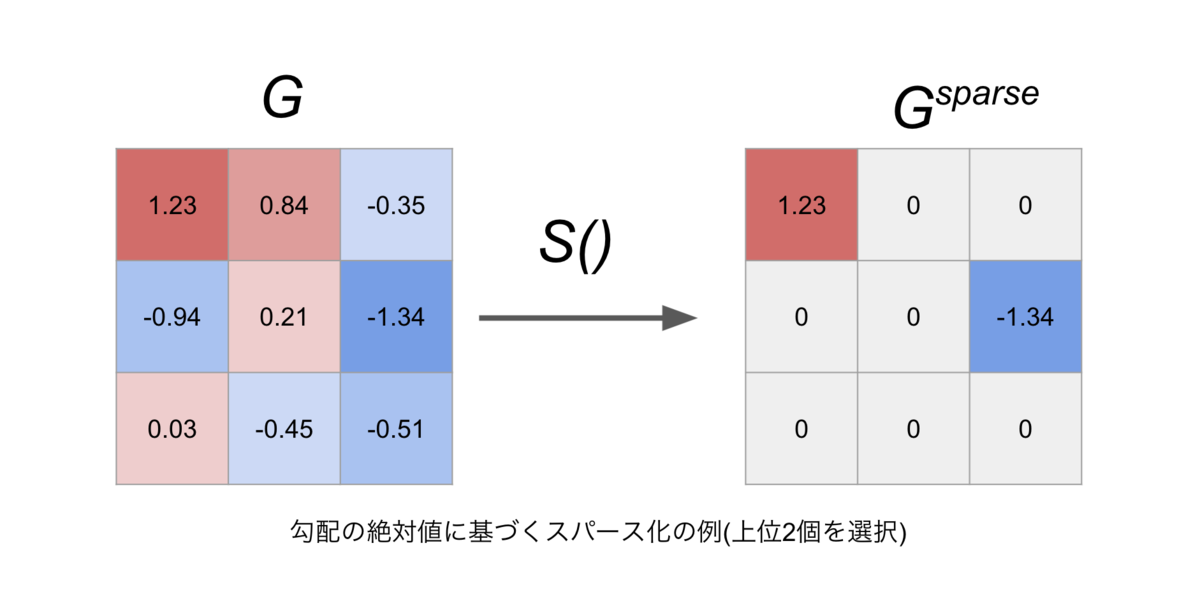
Gradient Sparsificationは,蓄積された結果十分に大きくなった勾配だけを同期ステップで通信するという手法です.代表例の一つとして,値の大きい順に上位 %を選択するTop-k Sparsificationがあります.
Gradient Quantization
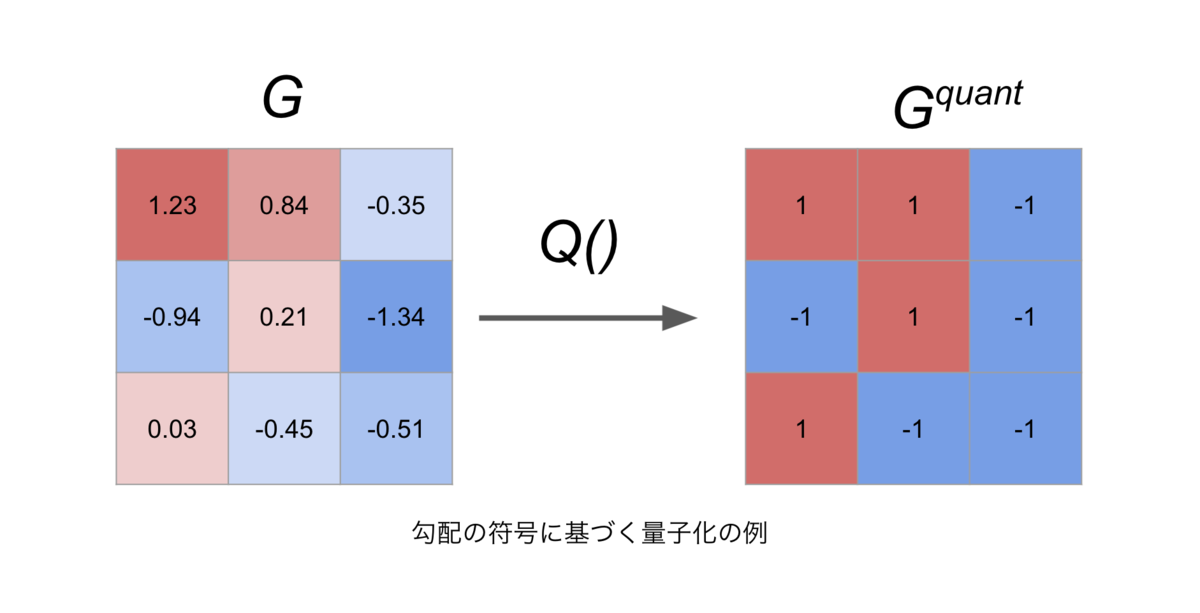
通常モデルの学習では,勾配には32ビット浮動小数点などが割り当てられますが,Gradient Quantizationではより粗い精度のデータ型を用いることで,勾配そのものの圧縮を試みます.例えば,32ビット浮動小数点の代わりに1ビットの整数を用いれば,勾配の通信量は32分の1に減少します.通信によって同期された勾配は,集約計算時に復元行列やスケーリング係数を用いて元の勾配とできるだけ近い形に変換される場合が多くあります.また,低精度で勾配を表現するという試みは,通信効率以外にもAdamのような最適化アルゴリズムとも関連しており,これらの分野からの研究アプローチもとられています.
Gradient Sparcification
Top-K S-SGD & global Top-K S-SGD
Top-K S-SGD [Aji et al., 2017]は,各ワーカーごとにTop-Kの大きさの勾配のみを通信するという非常にシンプルなアイディアで,後続の多くの研究がこのアプローチに倣っています.
さらに[Shi et al., 2019]では,各ワーカー間にも勾配の大きさに不均衡があるという観測から,ワーカー全体でTop-Kの勾配を通信するglobal Top-K S-SGDを提案しました.
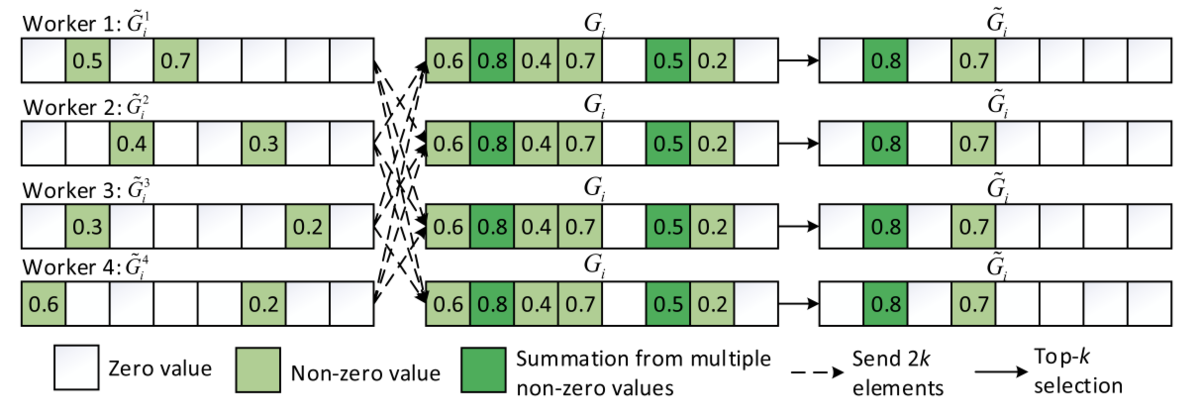
これらのフレームワークはシンプルながら強力であり,加えて多くの理論解析もなされています [Alistarh et al., 2018, Shi et al., 2019].
Gradient Quantization
1-bit SGD
2014年に提案された1-bit SGD[Seide et al., 2014]をはじめとして,様々な量子化手法が提案されています.1-bit SGDでは,通信を行う勾配の精度を1bitに減らすことで,学習速度を劇的に改善しました.この時,元の勾配と量子化後の誤差を最小にするような復元関数を作成して勾配と一緒に同期通信することで,集約時に復元します.また,量子化時に生じる誤差を次のイテレーションに繰り越して足し合わせる,Error Feedbackを用いることで,モデルの精度を維持することに成功しています.しかしこの論文では,1-bit SGDがある状況下で収束するということが実験的に示されただけで,その理論的な説明はありませんでした.
QSGD & TernGrad
のちの2017年には,QSGD[Alistarh et al., 2017]とTernGrad[Wen et al, 2017]と呼ばれる手法がそれぞれ収束レートについての理論解析付きで発表されました.この二つの手法の共通のポイントは,確率的な量子化を取り入れることによって,量子化後の勾配がバイアスを受けるのを防いでいる点です.
QSGDでは,量子化対象の勾配をL2正規化したものを,[0,1]の 分割されたレベルに近似します.この時,近いレベルに丸めるように近似するのではなく,両隣の近似レベルとの距離に基づく確率値によって近似レベルを決定します.これにより,勾配同期時にはベクトルの大きさ,ベクトルの各要素の符号,ベクトルの各要素の近似レベル(整数)のみを通信するだけで済むようになります.
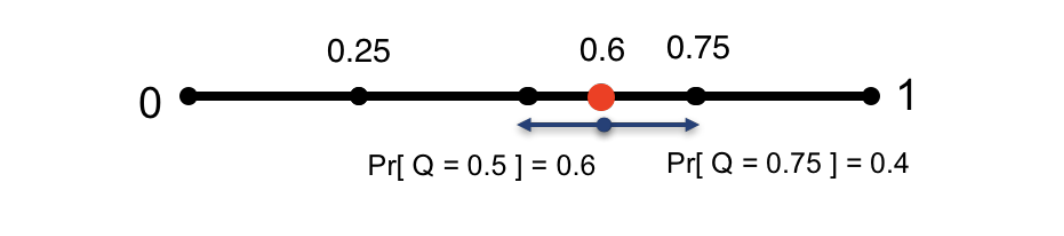
TernGradは,勾配を{0, ±1}の3段階と,勾配の絶対値の最大値であるスケール係数 で表現します.各勾配
は,確率
に従うベルヌーイ分布と自身の符号によって,0または±1に量子化されます.TernGradでは,理論解析における仮定部分にも勾配の絶対値の最大値が用いられており,この値が大きくなりすぎると性能を悪化させるとして,勾配のクリッピングとレイヤー毎での量子化も提案されています.
signSGD
また2018年には,勾配の持つ符号だけを用いてモデルの学習を行うsignSGD[Bernstein et al., 2018]が提案されました.QSGDやTernGradでは,量子化後の勾配がバイアスを持たないようにするために確率的な量子化アプローチがとられていますが,一方で勾配の分散を増大させるという深刻な問題も生じてしまいます.これを解決するために,signSGDでは勾配の集約時に符号の多数決を行う方法を提案しており,これはフル精度のSGDと比べて勾配の分散が同程度で済むことを理論的に示しました.
Error Feedback
Error Feedbackは,1-bit SGDでも用いられていた圧縮後の勾配の誤差を次のイテレーションに引き継ぐというテクニックです.[Sai et al.,2019]は,このError Feedbackについての理論解析に関する論文です.論文中では,signSGDは勾配の大きさと向きに関する多くの情報を失うことから強くバイアスを受けていると主張されており,signSGDがうまく収束しないコーナーケースも示されています.そのようなバイアスを持つ圧縮手法であっても,Error Feedback機構を導入することで元のSGDと同等の収束レートを達成することを示しました.実験では,Error Feedbackを持つsignSGDは元のSGDに近い収束レートであること,ミニバッチサイズに対してロバストな手法であることが示されています.
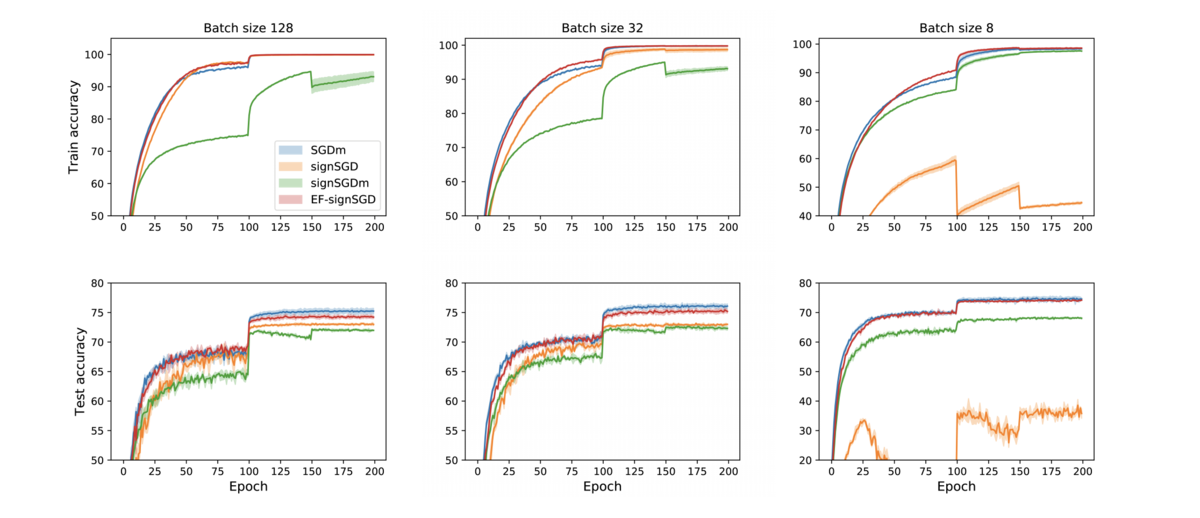
Fault Tolerance
複数ノードを用いる分散学習では,ビザンチン将軍問題のような,ノードの耐故障性についても問題となってきます.ビザンチン将軍問題とは,いくつかのノードが故障や外的要因によってでたらめな情報を出力してしまう場合(例えば符号ベースの量子化の場合,反転した符号など),クラスタ全体として正しい結果を維持できるかどうか,という問題です. [Bernstein et al, 2019]では,ノードに対する攻撃として,
- 勾配のスケールをランダムに変更する
- 勾配の符号を座標毎にランダムに変更する
- 勾配の推定値そのものを反転させる
の3つを挙げており,signSGDは各勾配が{-1, 1}のどちらかでしか表されないため,そのいずれに対してもロバストであると主張しています.また,故障しているノードが全体の %であるときの収束レートの上界を導出しました.
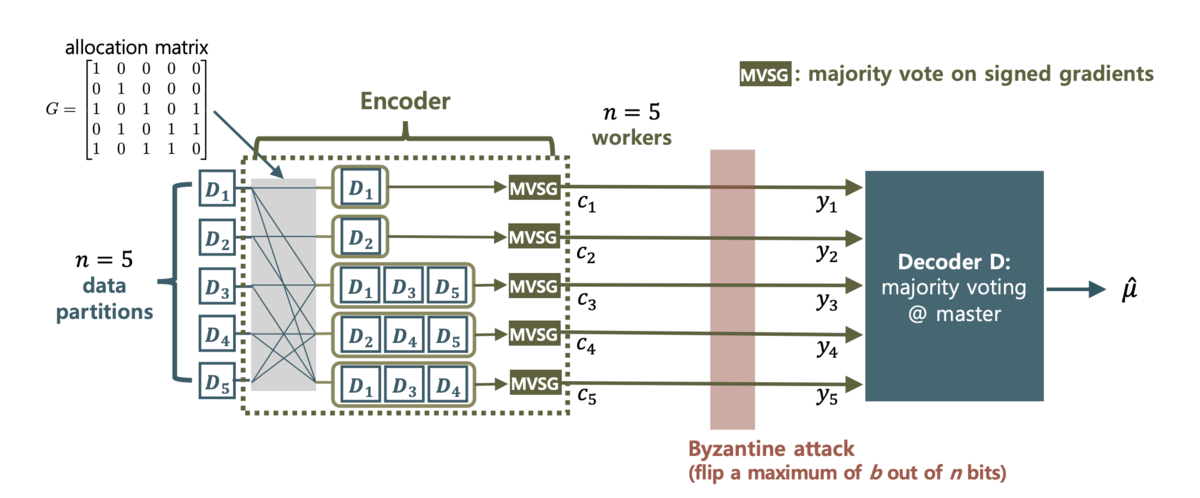
[Sohn et al, 2020]では,各ノードからパラメータサーバーに勾配を同期するときに,ノード間で勾配の中間集約を行うことで,ノード-パラメータサーバー間でのビザンチン将軍問題に対してロバストになるというアルゴリズムが提案されています.具体的には,allocation matrix の
成分が1ならば,ノードjで計算された勾配はノードiに渡され,ノード毎に中間集約を行います.論文では,Gの成分の決定方法として,ベルヌーイ分布による確率的な方法と,
ノード故障している時に完全に耐故障性を得る決定論的方法の2つが提案されています.
メタ研究
Gradient compressionに関連するメタ研究を一つ紹介します [Dutta et al., 2020]. 本研究では,gradient sparcification/quantizationの理論と実用の間に存在するギャップに焦点を当てています. 具体的には,多くのgradient compressionに関する理論的な結果はモデル全体の勾配が圧縮されることを仮定している一方で,実際の実装では各レイヤーごとに勾配の操作を行うことが多くなっています. これは主にフレームワークや実装上の都合に起因するものですが,当然気になるのはこのような理論と実装の間の差異は問題にならないのかという点です.
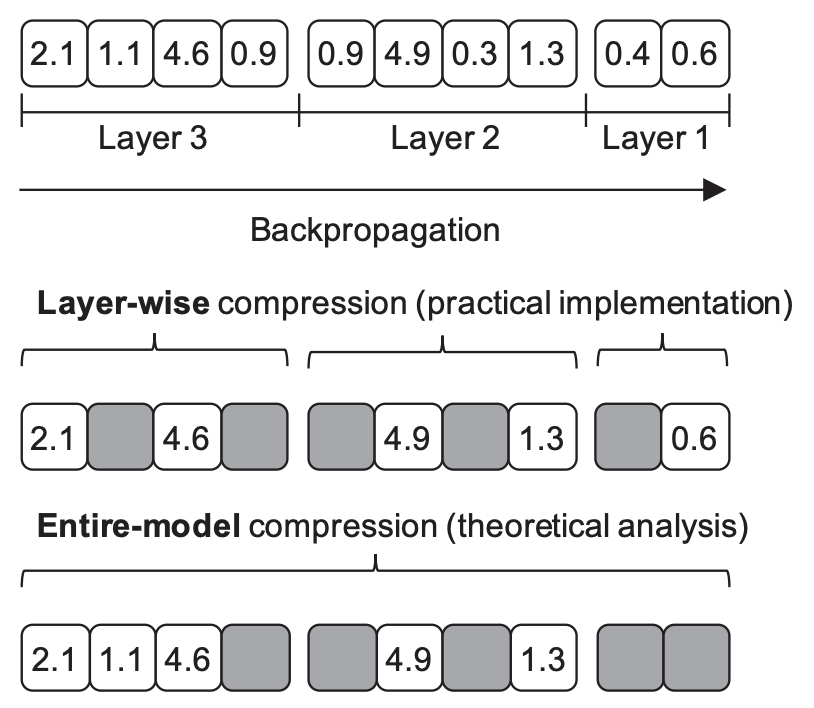
実際,モデル全体の勾配を圧縮する場合に成り立っていた収束レートに関する理論はレイヤーごとの圧縮においては成り立たないことが示されています. ただし面白いことに,本研究は同時にレイヤーごとの勾配圧縮に関する収束レートもまた別の理論展開で導出したところ,レイヤーごとの収束性に関する結果はモデル全体の勾配圧縮における結果と比べて悪くはないということが明らかになりました.
実際数値実験からも,むしろ多くの場合でレイヤーごとの圧縮の方が良かったとの報告がされています.
サーベイ
最後に,勾配圧縮に関するいくつかのサーベイ論文を紹介します.
- [Xu et al., 2020]
- [Ouyang et al., 2020]
- [Tang et al., 2020]
さいごに
Ridge-iでは様々なポジションで積極採用中です. カジュアル面談も可能ですので,ご興味がある方は是非ご連絡ください.
参考文献
- Aji, Alham Fikri, and Kenneth Heafield. "Sparse communication for distributed gradient descent." arXiv preprint arXiv:1704.05021 (2017).
- Lin, Yujun, et al. "Deep Gradient Compression: Reducing the Communication Bandwidth for Distributed Training." International Conference on Learning Representations. 2018.
- Shi, Shaohuai, et al. "A Convergence Analysis of Distributed SGD with Communication-Efficient Gradient Sparsification." IJCAI. 2019.
- Alistarh, Dan, et al. "The convergence of sparsified gradient methods." arXiv preprint arXiv:1809.10505 (2018).
- Alistarh, Dan, et al. "QSGD: Communication-efficient SGD via gradient quantization and encoding." Advances in Neural Information Processing Systems 30 (2017): 1709-1720.
- Seide, Frank, et al. "1-bit stochastic gradient descent and its application to data-parallel distributed training of speech dnns." Fifteenth Annual Conference of the International Speech Communication Association. 2014.
- Wen, Wei, et al. "TernGrad: ternary gradients to reduce communication in distributed deep learning." 31st International Conference on Neural Information Processing Systems (NIPS 2017). 2017.
- Bernstein, Jeremy, et al. "signSGD: Compressed optimisation for non-convex problems." International Conference on Machine Learning. PMLR, 2018.
- Karimireddy, Sai Praneeth, et al. "Error feedback fixes signsgd and other gradient compression schemes." International Conference on Machine Learning. PMLR, 2019.
- Shi, Shaohuai, et al. "A distributed synchronous SGD algorithm with global Top-k sparsification for low bandwidth networks." 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS). IEEE, 2019.
- Bernstein, Jeremy, et al. "signSGD with Majority Vote is Communication Efficient and Fault Tolerant." International Conference on Learning Representations. 2018.
- Sohn, Jy-yong, et al. "Election coding for distributed learning: Protecting SignSGD against byzantine attacks." Advances in Neural Information Processing Systems 33 (2020).
- Xu, Hang, et al. Compressed communication for distributed deep learning: Survey and quantitative evaluation. 2020.
- Ouyang, Shuo, et al. "Communication optimization strategies for distributed deep learning: A survey." arXiv preprint arXiv:2003.03009 (2020).
- Tang, Zhenheng, et al. "Communication-efficient distributed deep learning: A comprehensive survey." arXiv preprint arXiv:2003.06307 (2020).
- Dutta, Aritra, et al. "On the discrepancy between the theoretical analysis and practical implementations of compressed communication for distributed deep learning." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 34. No. 04. 2020.